一、是什么
冒泡排序(Bubble Sort),是一种计算机科学领域的较简单的排序算法
冒泡排序的思想就是在每次遍历一遍未排序的数列之后,将一个数据元素浮上去(也就是排好了一个数据)
如同碳酸饮料中二氧化碳的气泡最终会上浮到顶端一样,故名“冒泡排序”
假如我们要把 12、35、99、18、76 这 5 个数从大到小进行排序,那么数越大,越需要把它放在前面
思路如下:
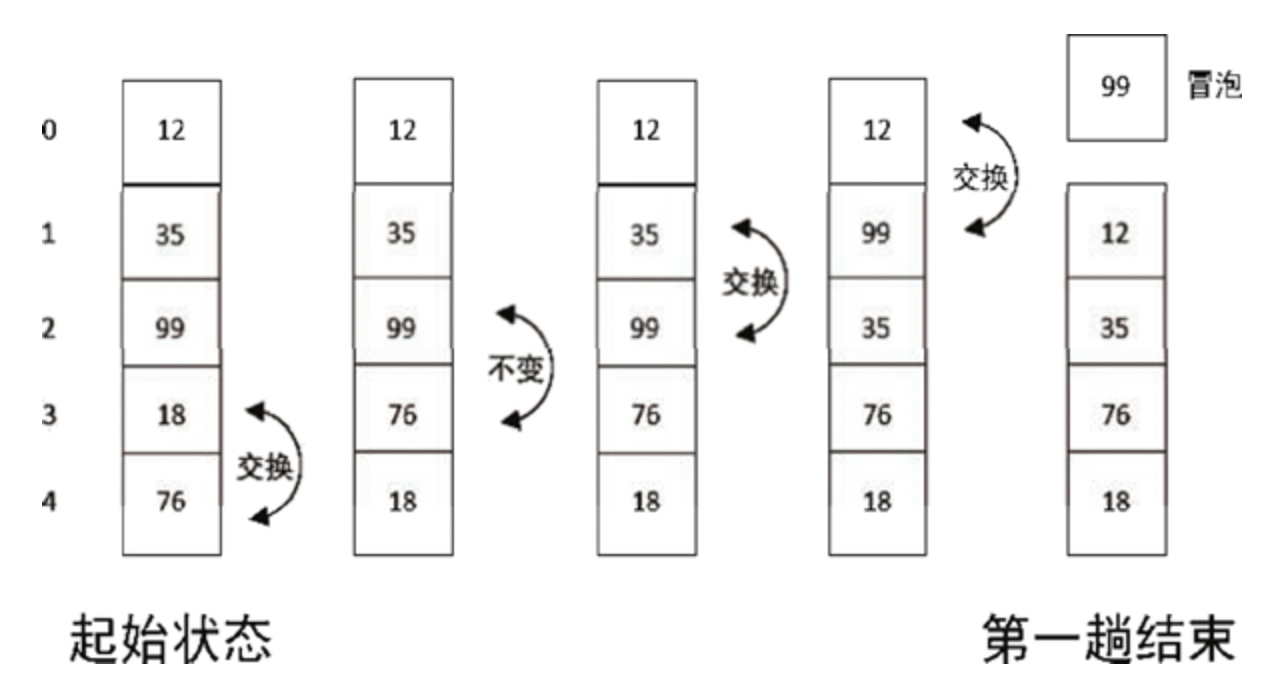
- 从后开始遍历,首先比较 18 和 76,发现 76 比 18 大,就把两个数交换顺序,得到 12、35、99、76、18
- 接着比较 76 和 99,发现 76 比 99 小,所以不用交换顺序
- 接着比较 99 和 35,发现 99 比 35 大,交换顺序
- 接着比较 99 和 12,发现 99 比 12 大,交换顺序
最终第 1 趟排序的结果变成了 99、12、35、76、18,如下图所示:
上述可以看到,经过第一趟的排序,可以得到最大的元素,接下来第二趟排序则对剩下的的4个元素进行排序,如下图所示:
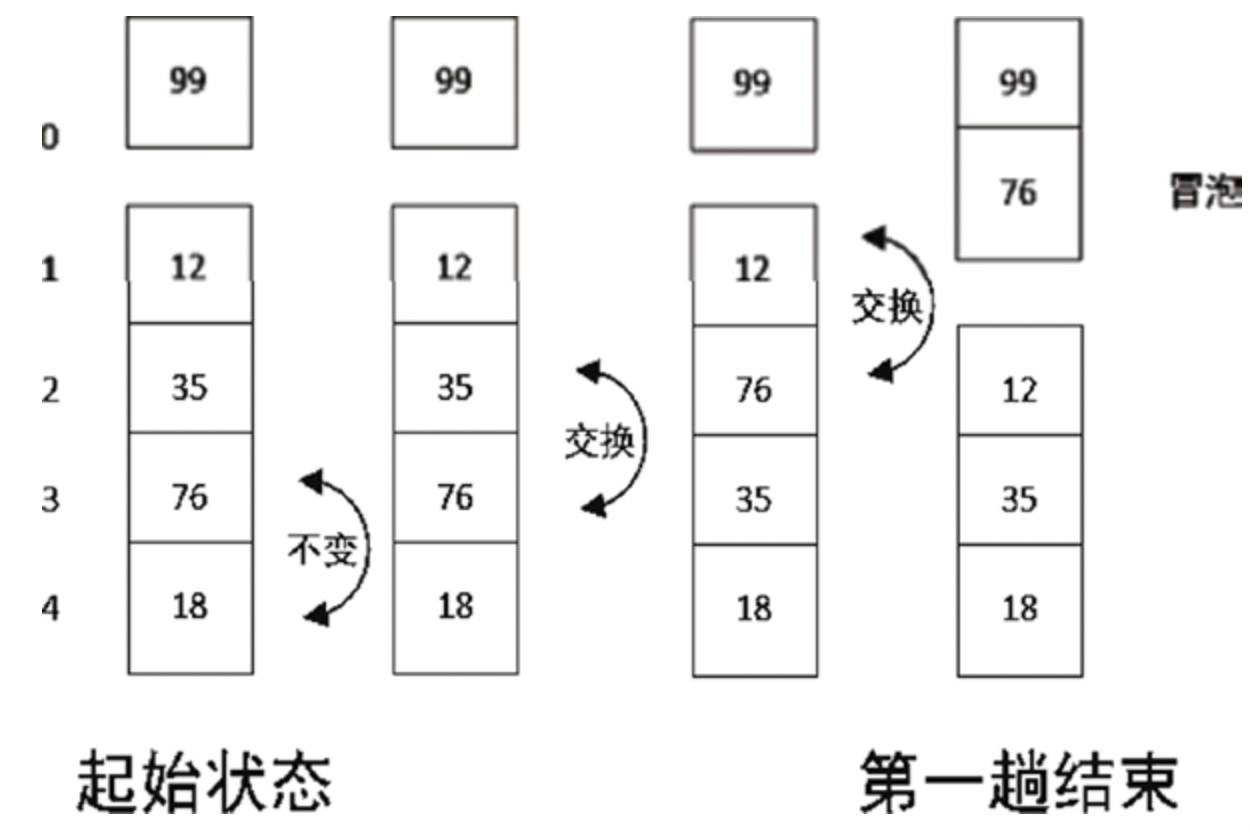
经过第 2 趟排序,结果为 99、76、12、35、18
然后开始第3趟的排序,结果为99、76、35、12、18
然后第四趟排序结果为99、76、35、18、12
经过 4 趟排序之后,只剩一个 12 需要排序了,这时已经没有可比较的元素了,这时排序完成
二、如何实现
如果要实现一个从小到大的排序,算法原理如下:
- 首先比较相邻的元素,如果第一个元素比第二个元素大,则交换它们
- 针对每一对相邻元素做同样的工作,从开始第一对到结尾的最后一对,这样,最后的元素回事最大的数
- 针对所有的元素重复以上的步骤,除了最后一个
- 持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较
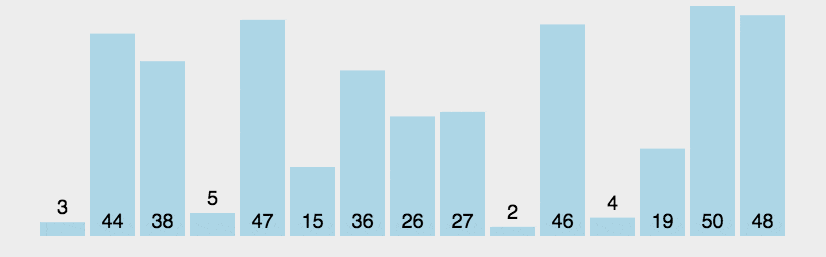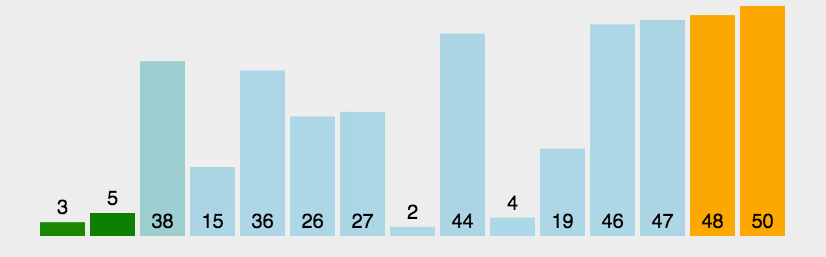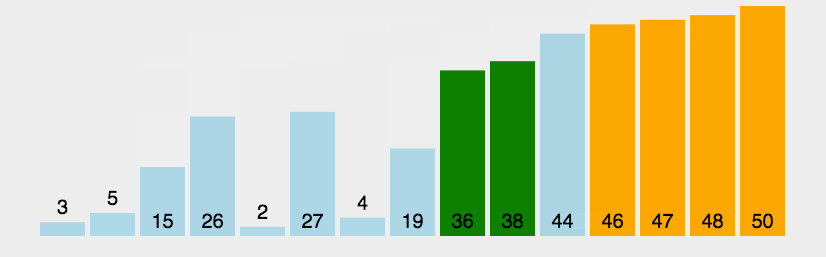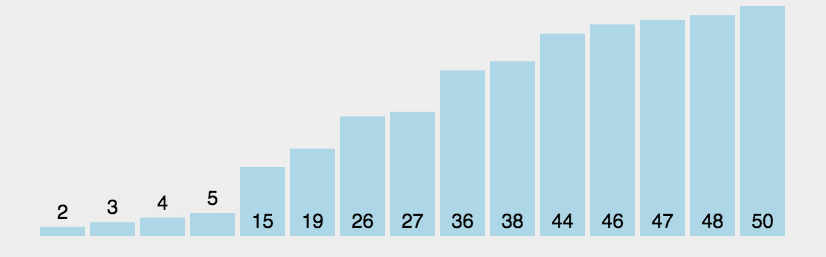
用代码表示则如下:
function bubbleSort(arr) {
const len = arr.length;
for (let i = 0; i < len - 1; i++) {
for (let j = 0; j < len - 1 - i; j++) {
if (arr[j] > arr[j+1]) { // 相邻元素两两对比
var temp = arr[j+1]; // 元素交换
arr[j+1] = arr[j];
arr[j] = temp;
}
}
}
return arr;
}
可以看到:冒泡排序在每一轮排序中都会使一个元素排到一趟, 也就是最终需要 n-1 轮这样的排序
而在每轮排序中都需要对相邻的两个元素进行比较,在最坏的情况下,每次比较之后都需要交换位置,此时时间复杂度为O(n^2)
优化
对冒泡排序常见的改进方法是加入一标志性变量exchange,用于标志某一趟排序过程中是否有数据交换
如果进行某一趟排序时并没有进行数据交换,则说明数据已经按要求排列好,可立即结束排序,避免不必要的比较过程
可以设置一标志性变量pos,用于记录每趟排序中最后一次进行交换的位置,由于pos位置之后的记录均已交换到位,故在进行下一趟排序时只要扫描到pos位置即可,如下:
function bubbleSort1(arr){
const i=arr.length-1;//初始时,最后位置保持不变
while(i>0){
let pos = 0;//每趟开始时,无记录交换
for(let j = 0; j < i; j++){
if(arr[j] > arr[j+1]){
let tmp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = tmp;
pos = j;//记录最后交换的位置
}
}
i = pos;//为下一趟排序作准备
}
return arr;
}
在待排序的数列有序的情况下,只需要一轮排序并且不用交换,此时情况最好,时间复杂度为O(n)
并且从上述比较中看到,只有后一个元素比前面的元素大(小)时才会对它们交换位置并向上冒出,对于同样大小的元素,是不需要交换位置的,所以对于同样大小的元素来说,相对位置是不会改变的,因此, 冒泡排序是稳定的
三、应用场景
冒泡排的核心部分是双重嵌套循环, 时间复杂度是 O(N 2 ),相比其它排序算法,这是一个相对较高的时间复杂度,一般情况不推荐使用,由于冒泡排序的简洁性,通常被用来对于程序设计入门的学生介绍算法的概念
参考文献
- https://baike.baidu.com/item/%E5%86%92%E6%B3%A1%E6%8E%92%E5%BA%8F/4602306
- https://www.runoob.com/w3cnote/bubble-sort.html
- http://data.biancheng.net/view/116.html
- https://dsb123dsb.github.io/2017/03/07/js%E5%AE%9E%E7%8E%B0%E5%86%92%E6%B3%A1%E6%8E%92%E5%BA%8F%E4%BB%A5%E5%8F%8A%E4%BC%98%E5%8C%96/



 表情
表情